Kurioses: eine Logarithmentafel im Westentaschenformat

Als ich zur Schule ging, waren Taschenrechner nicht erfunden, es wurde noch der Umgang mit dem Rechenschieber gelehrt, und wer etwas größere Präzision brauchte, mußte auf die Logarithmentafel zurückgreifen.

In unserer mathematisch-naturwissenschaftlichen Formel- und Tabellensammlung, dem "Tafelwerk", wurden den dekadischen Logarithmen ganze zwei Seiten eingeräumt - sie erlaubten also nur das Aufsuchen dreistelliger Numeri.

Zwar besaß ich auch eine fünfstellige Logarithmentafel aus dem Familienerbe (für Numeri mit bis zu 4 Ziffern), aber die hatte Quartformat und wog ein halbes Kilo, nichts für unterwegs und alle Tage! Allerdings hat diese Tafel wohl gewissen historischen Wert, ist sie doch 1911 in bereits 111. Auflage herausgegeben.

In Vorwegnahme der Idee des Taschenrechners beschloß ich als angehender Student 1974, mir eine fünfstellige Logarithmentafel im Westentaschenformat herzustellen. Zupaß kam mir dabei, daß ich mich schon in den oberen Schulklassen ausgiebig mit der dualen Codierung von Zahlen, z.B. auf dem Lochstreifen, befaßt hatte: 4 Bits reichen für die Darstellung der Ziffern von 0 bis 9; und wie aus einem Bitmuster auf die zugehörige Ziffer rückgeschlossen werden kann, war mir in Fleisch und Blut übergegangen.

Ein Bit aber braucht keine Form wie eine Ziffer, die sich nicht beliebig verkleinern und - in mikroskopischer Größe - dann wieder nicht lesen ließe; für ein Bit reicht ein Punkt!

Hier bot sich also eine Lösung an, die Logarithmentafel zu schrumpfen, ohne auf unüberwindliche Herstellungsprobleme zu stoßen oder ihre Lesbarkeit (für den Eingeweihten) zu schmälern.

Räumt man jedem Punkt einen Quadratmillimeter ein, so ist er von seinen Nachbarn ausgezeichnet unterscheidbar, und eine Ziffer braucht nur noch eine millimeterhohe Zeile. Auf einer 10 Zentimeter hohen Seite bringt man 100 Zeilen unter, also bereits zwei Dezimalen des Numerus. Für die vierstelligen Numeri der Gauß'schen Tafel würden mithin 100 Seiten reichen, d.h. ein Büchlein mit 50 Blatt.

Ich habe dann tatsächlich die Gauß'sche Logarithmentafel auf Millimeterpapier "abgeschrieben" - mit Punktemustern für die zwei letzten Ziffern der Mantisse (wahrscheinlich habe ich über weite Strecken auch jemanden aus der Familie zum Ansagen gewinnen können), habe die Seiten außen und unten mit einem Griffregister versehen und das Ganze mit einer selbstgemachten Rückenklebung zum Büchlein gebunden.
Offenbar habe ich diese Tafel auch tatsächlich benutzt - die Spuren an der Griffleiste deuten darauf hin, obwohl ich mich nicht konkret erinnern kann.

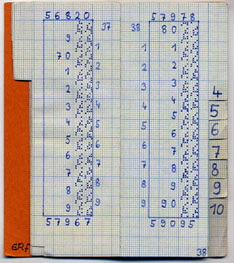
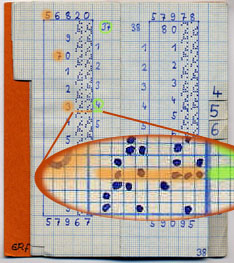
Die farbigen Hervorhebungen verdeutlichen, wie man die Tafel liest: lg(3.746) = 0.57357 - der Numerus wird auf der inneren Spalte aufgesucht, wozu man mittels der Griffleiste an der Seitenunterkante die Seite -37- aufschlägt; die folgende Ziffer -4- ist noch als Zahl notiert, während die letzte -6- die Millimeter-Zeile bezeichnet, auf der der Tafelwert abgelesen werden muß. (Die Zählung beginnt natürlich bei Null!)
Den Logarithmus setzt man aus den vorhandenen Ziffern (führende drei Stellen -5-7-3-) und den zwei decodierten Punktmustern in der bezeichneten Millimeter-Zeile (-5- und -7-) zusammen.

Wenig später wurde mir mein erster Taschenrechner geschenkt, mit "umgekehrt polnischer Notation" und sogar einem 52 Befehle tiefen Programmspeicher.

Er besaß aber keine bedingten Sprungfunktionen und nur einen Speicherplatz, weshalb ich in den Folgejahren damit beschäftigt war, die systemeigenen Fehler oder Schranken dieses Rechners, z.B. seine Rechengenauigkeit, für diese Zwecke zu mißbrauchen - das aber ist dann bereits ein anderes Kapitel.

© by , 02-apr-04,
Last revised: